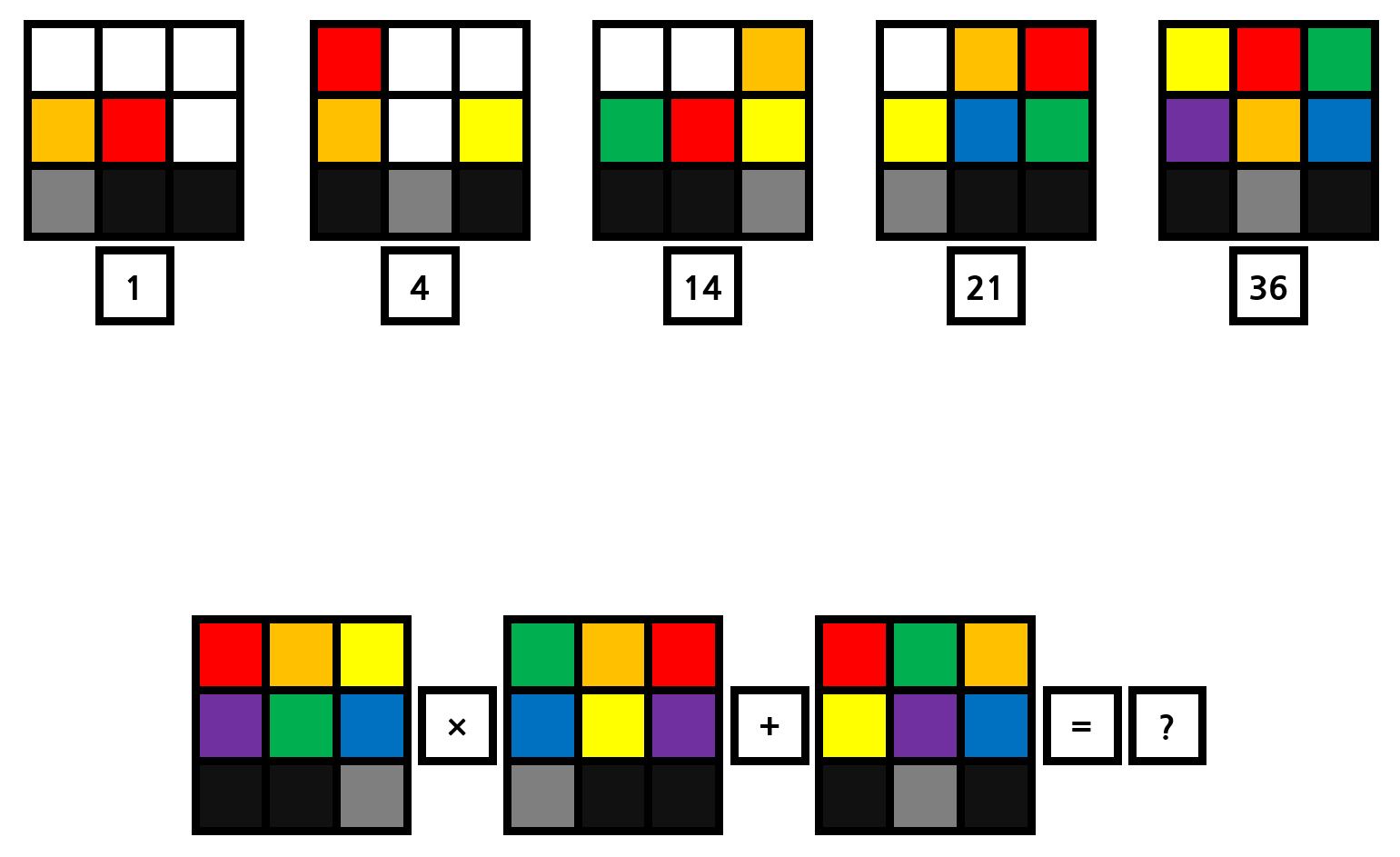
주어진 컬러풀 네모에 대한 정보를 토대로 하단의 수식의 결과값을 예측하여라.
* 단, 정답이 숫자의 형태이므로, 정확한 채점을 위해(브루트 포스 방지용) 다음의 입력 형식을 지켜야 한다.
위 계산식에서 (첫 번째 네모의 값)/(두 번째 네모의 값)/(세 번째 네모의 값)/(최종 계산 결과 값) 으로 표기하길 바란다.
가령 주어진 도형의 치환값이 각각 12345, 23456, 34567 이라고 하면,
계산값은 12345*23456+34567 = 289598887이므로
12345/23456/34567/289598887 라고 적으면 된다.
* 모든 값은 적어도 음수는 아니며, 각각 2^12-1보다는 작은 값임을 숙지하여라.
HINT : 

58/57/30/3336
* 하노이의 탑
1행, 2행 => 하노이의 원판
3행 => 하노이 바닥, 회색으로 모든 원판을 모으는 것이 목적.
( 하노이의 탑의 규칙을 모른다면 구글링 참고. )
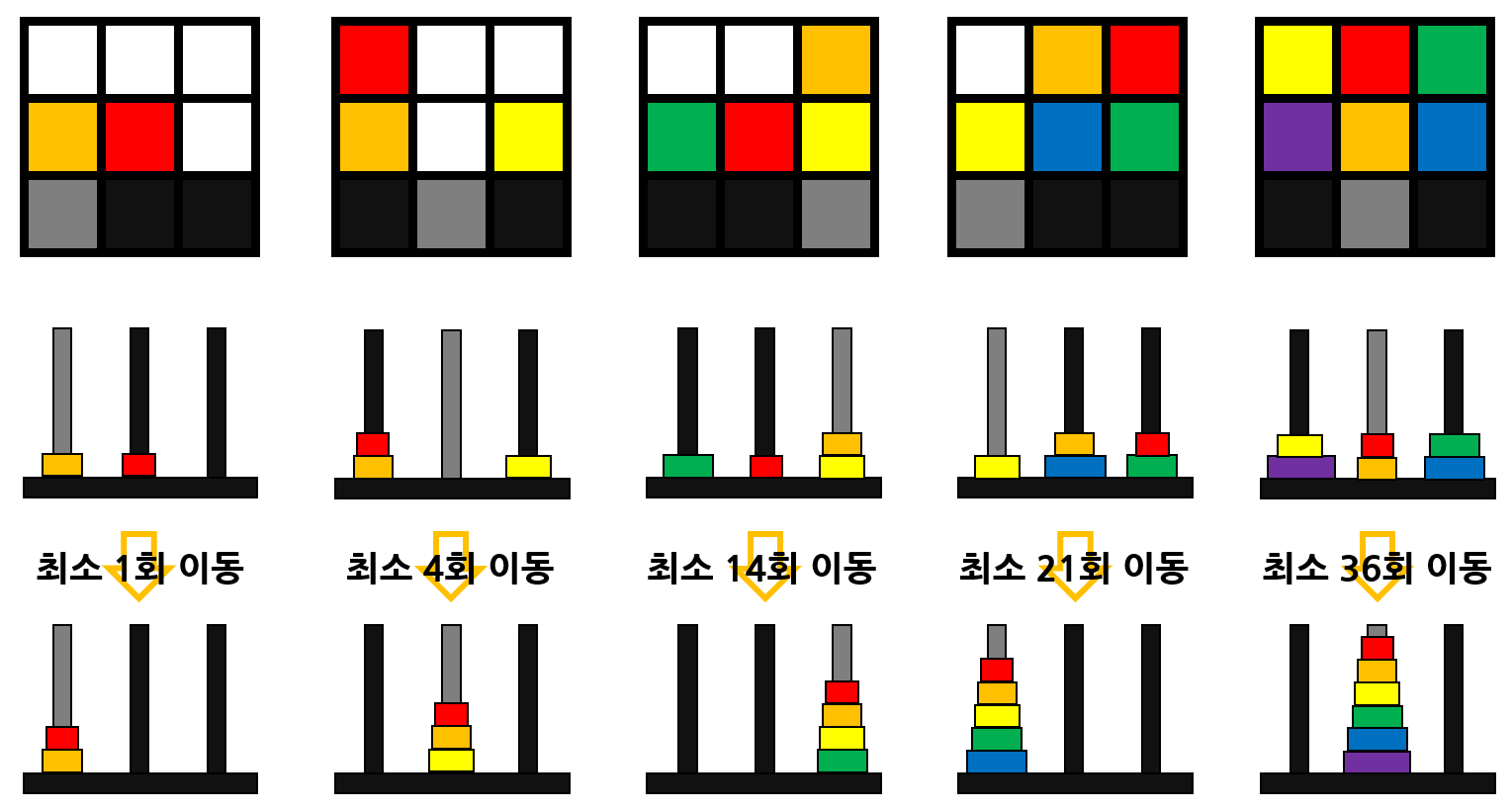
위 그림은 맨 처음의 5개의 규칙에 대한 변환 형태.
적색 -> 주황색 -> 노랑 -> 초록 -> 파랑 -> 보라색의 원판 순서대로 점점 크기가 커지는 것이 핵심.
회색 기둥으로 모든 원판을 모은다고 했을 때 최소 이동횟수를 구하는 것이 관건.
규칙을 유추할 수 있도록 기본적인 하노이의 탑 형태의 일부 과정에서 출발하도록 문제를 구성하였음.
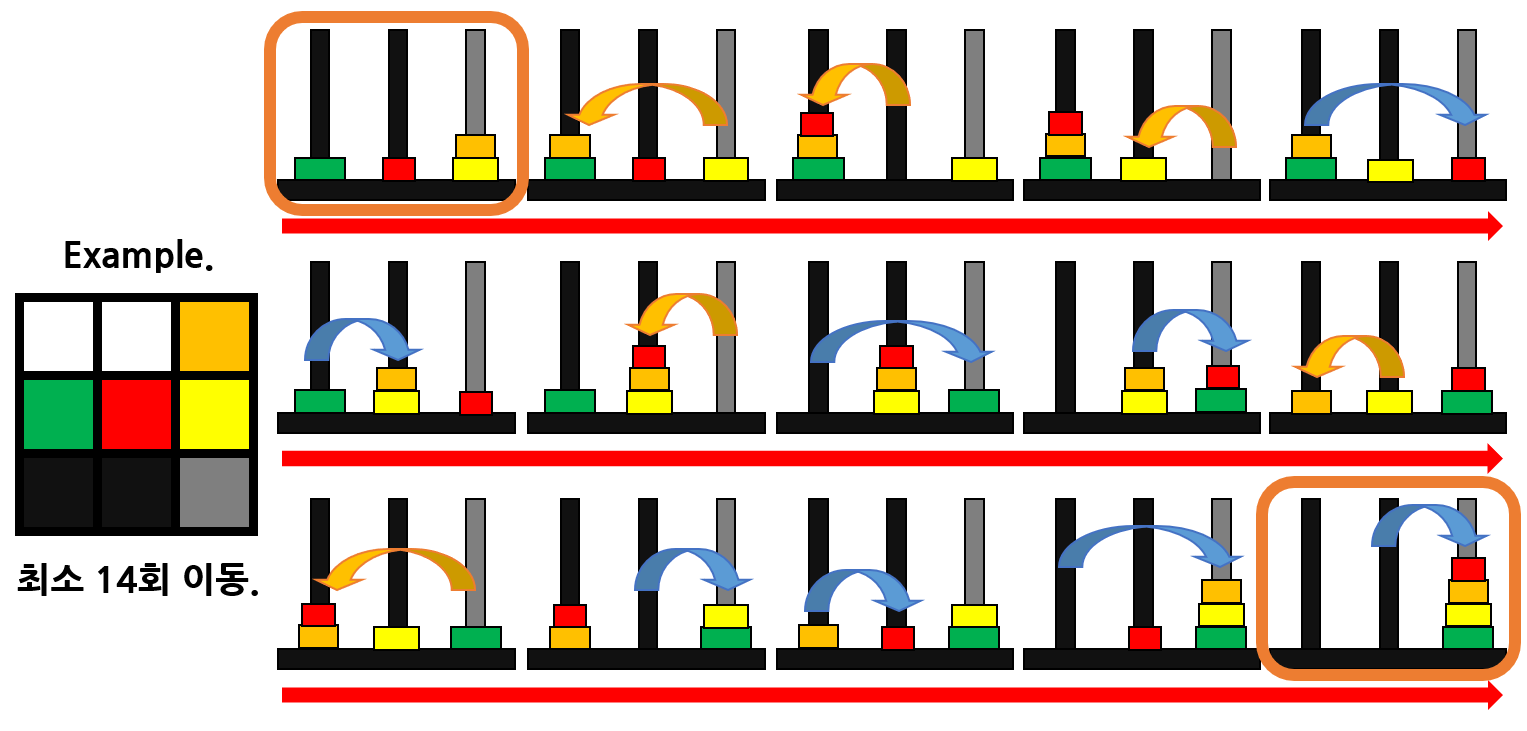
위 그림은 14라고 적힌 그림의 예시.
다음과 같이 적어도 14번의 원판을 움직여야 다음과 같이 정렬할 수 있다.
따라서 위 그림은 14라는 값을 갖는다고 볼 수 있다.
그 외의 그림에 대해서는 귀납적으로 수행하면 최소 이동횟수를 얻어낼 수 있으므로 그림 상에선 생략.
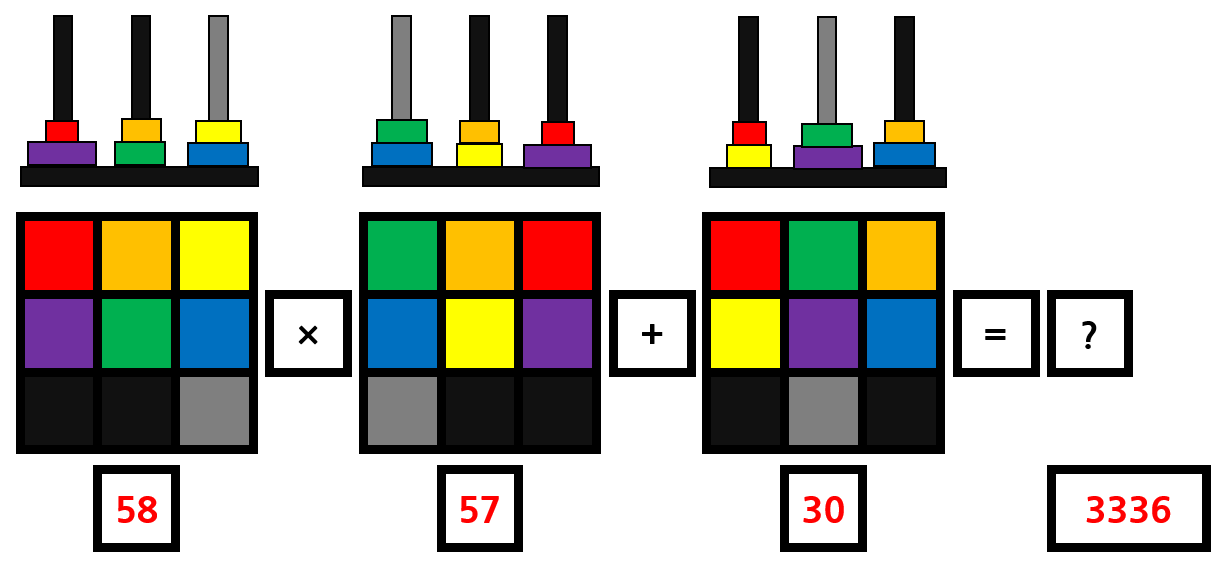
최종 하단식에서의 결과 값.
위 6개의 원판에 대한 시행은 일반적인 하노이 게임에선 얻을 수 없으며,
문제 출제를 위해 만든 특수한 형태의 출발선이라 볼 수 있다.
결국, 58*57+30의 값은 3336이므로 정답은 '58/57/30/3336'의 값으로 나오게 된다.
// =========== 위 문제의 결과값을 얻기 위한 심화 이론 ===========
하노이의 탑에서의 각 원판 상태를 그래프에 대응시키면
시에르핀스키 삼각형(sierpinski triangle)의 형태로 대응이 되는 것을 확인할 수 있다.
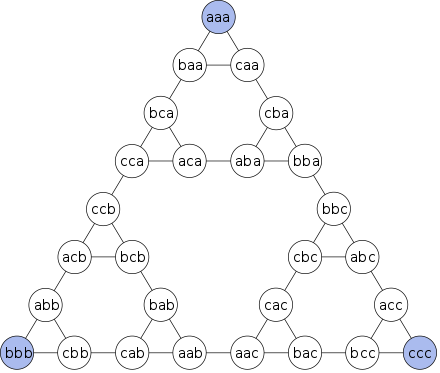
[ * reference - https://en.wikipedia.org/wiki/Tower_of_Hanoi ]
위 그림은 원판의 개수가 3개일 때의 상태를 나타낸 형태이다.
각 기둥을 좌에서 우 순서로 a, b, c라 대응하고,
주어진 상태는 1번째 원판의 위치/2번째 원판의 위치/3번째 원판의 위치 를 상징한다.
즉, 위 그림에서 abc가 의미하는 바는, 좌측 A기둥에 1번원판, 중간 B 기둥에 2번원판, 우측 C기둥에 3번원판이 있는 상태이다.
결과적으로 일반화 된 하노이의 탑 게임은 aaa, bbb, ccc로 가는 것이 목적인데,
어디를 목표로 하느냐에 따라 최소거리가 달라지게 된다.
가령, abc에서 aaa로 간다고 하면,
abc -> bbc -> bba -> cba -> caa -> aaa 순서로 원판을 옮기면 된다.
앞서 문제에서 4라는 값을 지닌 하노이의 탑을 위 형태로 치환하면 aac에서 bbb로 가기 위한 최소 이동 수라고 볼 수 있다.
즉, aac -> aab -> cab -> cbb -> bbb로 총 4번을 가게 된다는 것을 알 수 있다.
위 형태를 이용하면 고차원의 형태에 대한 일반화 된 최소경로를 구할 수 있을 것이다.
위 고차원의 형태에서 최단이동횟수를 구하는 프로그램은 하단의 레퍼런스를 참고하면 된다.
[ * reference - https://mathematica.stackexchange.com/questions/160753/ ]
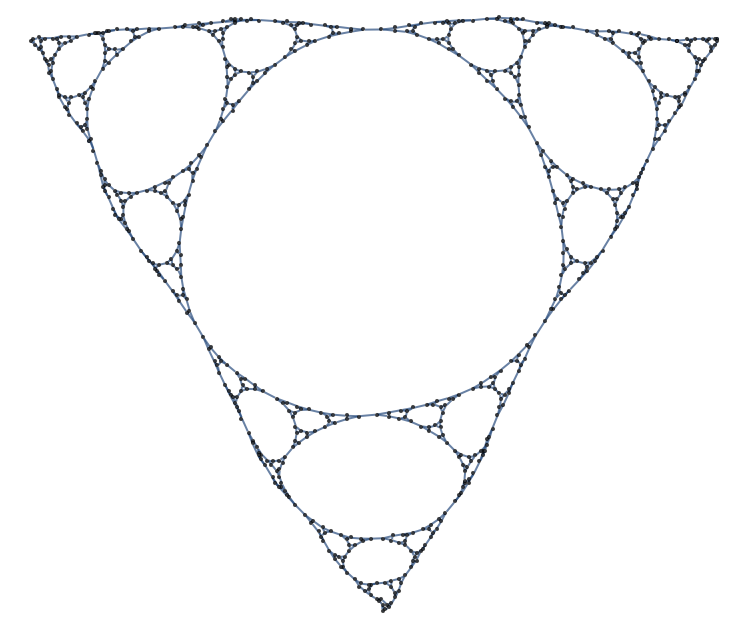
주어진 문제는 n=6일때의 하노이 삼각형을 구해서 최단경로를 물색하는 것이 목적이다.
그리고 n=6일때의 하노이 삼각형은 위의 형태로 나타나게 된다.
(위 그림은 앞선 레퍼런스에서 나온 시각화 된 그림이다.)
해당 레퍼런스에서 개발자 Vasily Mitch분의 코드를 활용하면, 최소 이동 과정을 확인할 수 있다.
가령 주어진 레퍼런스에선 1,2 // 4,6 // 3,5 에서 시작해서 2,6 // 3,5 // 1,4로 종료한다고 했을 때의
최소이동과정을 계산해주고 있는데, 결과가 조금 복잡하긴 하다.
{{{1, 2}, {4, 6}, {3, 5}}, {{2}, {4, 6}, {1, 3, 5}}, {{}, {2, 4, 6}, {1, 3, 5}}, {{}, {1, 2, 4, 6}, {3, 5}},
{{3}, {1, 2, 4, 6}, {5}}, {{3}, {2, 4, 6}, {1, 5}}, {{2, 3}, {4, 6}, {1, 5}}, {{1, 2, 3}, {4, 6}, {5}},
{{1, 2, 3}, {6}, {4, 5}}, {{2, 3}, {6}, {1, 4, 5}}, {{3}, {2, 6}, {1, 4, 5}}, {{3}, {1, 2, 6}, {4, 5}},
{{}, {1, 2, 6}, {3, 4, 5}}, {{1}, {2, 6}, {3, 4, 5}}, {{1}, {6}, {2, 3, 4, 5}}, {{}, {6}, {1, 2, 3, 4, 5}},
{{6}, {}, {1, 2, 3, 4, 5}}, {{6}, {1}, {2, 3, 4, 5}}, {{2, 6}, {1}, {3, 4, 5}}, {{1, 2, 6}, {}, {3, 4, 5}},
{{1, 2, 6}, {3}, {4, 5}}, {{2, 6}, {3}, {1, 4, 5}}, {{6}, {2, 3}, {1, 4, 5}}, {{6}, {1, 2, 3}, {4, 5}},
{{4, 6}, {1, 2, 3}, {5}}, {{1, 4, 6}, {2, 3}, {5}}, {{1, 4, 6}, {3}, {2, 5}}, {{4, 6}, {3}, {1, 2, 5}},
{{3, 4, 6}, {}, {1, 2, 5}}, {{3, 4, 6}, {1}, {2, 5}}, {{2, 3, 4, 6}, {1}, {5}}, {{1, 2, 3, 4, 6}, {}, {5}},
{{1, 2, 3, 4, 6}, {5}, {}}, {{2, 3, 4, 6}, {1, 5}, {}}, {{3, 4, 6}, {1, 5}, {2}}, {{3, 4, 6}, {5}, {1, 2}},
{{4, 6}, {3, 5}, {1, 2}}, {{1, 4, 6}, {3, 5}, {2}}, {{1, 4, 6}, {2, 3, 5}, {}}, {{4, 6}, {1, 2, 3, 5}, {}},
{{6}, {1, 2, 3, 5}, {4}}, {{6}, {2, 3, 5}, {1, 4}}, {{2, 6}, {3, 5}, {1, 4}}}
Wolfram에서의 Length함수를 이용해서 위 길이를 구하면, 42의 값이 나온다.
(* 단, 시작점도 포함되어 있으므로, 결과값에 -1을 해줘야 한다.)
즉, 1,2 // 4,6 // 3,5 -> 2,6 // 3,5 // 1,4로 가기 위해선 최소 42번의 이동이 필요하게 된다.
이제 주어진 문제에서의 결과를 위 코드를 활용하여 계산하기만 하면 된다.
각 3개의 임의의 하노이 도식에 대한 내용은 다음과 같다.
* 1,6 // 2,4 // 3,5 -> x // x // 1,2,3,4,5,6
{{{1,6},{2,4},{3,5}},{{1,6},{4},{2,3,5}},{{6},{4},{1,2,3,5}},{{4,6},{},{1,2,3,5}},{{1,4,6},{},{2,3,5}},
{{1,4,6},{2},{3,5}},{{4,6},{1,2},{3,5}},{{3,4,6},{1,2},{5}},{{3,4,6},{2},{1,5}},{{2,3,4,6},{},{1,5}},
{{1,2,3,4,6},{},{5}},{{1,2,3,4,6},{5},{}},{{2,3,4,6},{5},{1}},{{3,4,6},{2,5},{1}},{{3,4,6},{1,2,5},{}},
{{4,6},{1,2,5},{3}},{{1,4,6},{2,5},{3}},{{1,4,6},{5},{2,3}},{{4,6},{5},{1,2,3}},{{6},{4,5},{1,2,3}},
{{6},{1,4,5},{2,3}},{{2,6},{1,4,5},{3}},{{1,2,6},{4,5},{3}},{{1,2,6},{3,4,5},{}},{{2,6},{3,4,5},{1}},
{{6},{2,3,4,5},{1}},{{6},{1,2,3,4,5},{}},{{},{1,2,3,4,5},{6}},{{},{2,3,4,5},{1,6}},{{2},{3,4,5},{1,6}},
{{1,2},{3,4,5},{6}},{{1,2},{4,5},{3,6}},{{2},{1,4,5},{3,6}},{{},{1,4,5},{2,3,6}},{{},{4,5},{1,2,3,6}},
{{4},{5},{1,2,3,6}},{{1,4},{5},{2,3,6}},{{1,4},{2,5},{3,6}},{{4},{1,2,5},{3,6}},{{3,4},{1,2,5},{6}},
{{3,4},{2,5},{1,6}},{{2,3,4},{5},{1,6}},{{1,2,3,4},{5},{6}},{{1,2,3,4},{},{5,6}},{{2,3,4},{1},{5,6}},
{{3,4},{1},{2,5,6}},{{3,4},{},{1,2,5,6}},{{4},{3},{1,2,5,6}},{{1,4},{3},{2,5,6}},{{1,4},{2,3},{5,6}},
{{4},{1,2,3},{5,6}},{{},{1,2,3},{4,5,6}},{{},{2,3},{1,4,5,6}},{{2},{3},{1,4,5,6}},{{1,2},{3},{4,5,6}},
{{1,2},{},{3,4,5,6}},{{2},{1},{3,4,5,6}},{{},{1},{2,3,4,5,6}},{{},{},{1,2,3,4,5,6}}}
=> 58번 이동.
* 4,5 // 2,3 // 1,6 -> 1,2,3,4,5,6 // x // x
{{{4,5},{2,3},{1,6}},{{4,5},{1,2,3},{6}},{{5},{1,2,3},{4,6}},{{5},{2,3},{1,4,6}},{{2,5},{3},{1,4,6}},
{{1,2,5},{3},{4,6}},{{1,2,5},{},{3,4,6}},{{2,5},{1},{3,4,6}},{{5},{1},{2,3,4,6}},{{5},{},{1,2,3,4,6}},
{{},{5},{1,2,3,4,6}},{{1},{5},{2,3,4,6}},{{1},{2,5},{3,4,6}},{{},{1,2,5},{3,4,6}},{{3},{1,2,5},{4,6}},
{{3},{2,5},{1,4,6}},{{2,3},{5},{1,4,6}},{{1,2,3},{5},{4,6}},{{1,2,3},{4,5},{6}},{{2,3},{1,4,5},{6}},
{{3},{1,4,5},{2,6}},{{3},{4,5},{1,2,6}},{{},{3,4,5},{1,2,6}},{{1},{3,4,5},{2,6}},{{1},{2,3,4,5},{6}},
{{},{1,2,3,4,5},{6}},{{6},{1,2,3,4,5},{}},{{1,6},{2,3,4,5},{}},{{1,6},{3,4,5},{2}},{{6},{3,4,5},{1,2}},
{{3,6},{4,5},{1,2}},{{3,6},{1,4,5},{2}},{{2,3,6},{1,4,5},{}},{{1,2,3,6},{4,5},{}},{{1,2,3,6},{5},{4}},
{{2,3,6},{5},{1,4}},{{3,6},{2,5},{1,4}},{{3,6},{1,2,5},{4}},{{6},{1,2,5},{3,4}},{{1,6},{2,5},{3,4}},
{{1,6},{5},{2,3,4}},{{6},{5},{1,2,3,4}},{{5,6},{},{1,2,3,4}},{{5,6},{1},{2,3,4}},{{2,5,6},{1},{3,4}},
{{1,2,5,6},{},{3,4}},{{1,2,5,6},{3},{4}},{{2,5,6},{3},{1,4}},{{5,6},{2,3},{1,4}},{{5,6},{1,2,3},{4}},
{{4,5,6},{1,2,3},{}},{{1,4,5,6},{2,3},{}},{{1,4,5,6},{3},{2}},{{4,5,6},{3},{1,2}},{{3,4,5,6},{},{1,2}},
{{3,4,5,6},{1},{2}},{{2,3,4,5,6},{1},{}},{{1,2,3,4,5,6},{},{}}}
=> 57번 이동
* 1,3 // 4,6 // 2,5 -> x // 1,2,3,4,5,6 // x
{{{1,3},{4,6},{2,5}},{{1,3},{2,4,6},{5}},{{3},{1,2,4,6},{5}},{{},{1,2,4,6},{3,5}},{{1},{2,4,6},{3,5}},
{{1},{4,6},{2,3,5}},{{},{4,6},{1,2,3,5}},{{4},{6},{1,2,3,5}},{{1,4},{6},{2,3,5}},{{1,4},{2,6},{3,5}},
{{4},{1,2,6},{3,5}},{{3,4},{1,2,6},{5}},{{3,4},{2,6},{1,5}},{{2,3,4},{6},{1,5}},{{1,2,3,4},{6},{5}},
{{1,2,3,4},{5,6},{}},{{2,3,4},{5,6},{1}},{{3,4},{2,5,6},{1}},{{3,4},{1,2,5,6},{}},{{4},{1,2,5,6},{3}},
{{1,4},{2,5,6},{3}},{{1,4},{5,6},{2,3}},{{4},{5,6},{1,2,3}},{{},{4,5,6},{1,2,3}},{{},{1,4,5,6},{2,3}},
{{2},{1,4,5,6},{3}},{{1,2},{4,5,6},{3}},{{1,2},{3,4,5,6},{}},{{2},{3,4,5,6},{1}},{{},{2,3,4,5,6},{1}},
{{},{1,2,3,4,5,6},{}}}
=> 30번 이동
각각 58, 57, 30의 값을 얻을 수 있게 된다.
( 다시 한번 개발자 Vasily Mitch분에게 감사의 말씀을 드립니다. )
* 주석 // 초기 문제에서 값의 범위를 9^81보다 작다고 산정한 이유는 만일을 위한 브루트포스 방지용으로 넣은 심리적 문구이다.
( min~max 사이로 브루프토스 기법을 이용해서 클리어하는 편법을 누군가 쓸 것 같아서 정답과는 무관한 아주 큰 값으로 정했다. )
( 그니까 쉽게 말해 맥거핀이다. )
